After I started posting weekly Equity and Pot Odds quizzes on my Instagram page(@thepokermindset), I’ve got asked a lot how to calculate them, so I’ve decided to write a short article about it.
If you’re unfamiliar with the mathematics of poker and you’re wondering if you can get by without learning it, then understand that ignoring the mathematical side of poker will leave you with a massive disadvantage. Poker is not only about tells, reads and ‘feel’, and if you don’t know how to calculate pot odds I guarantee that you are burning money at the poker tables. My advice: Stop making the excuse that math wasn’t your favorite subject in school. Don’t be lazy and do the work!
You do not need a PhD in Mathematics to be able to calculate pot odds. All you need is middle school math knowledge and you’re good to go.
Odds, probability and statistics are attached to every aspect of your game, it can be your actions, the hands you play, your bet, anything.
I would say one of the fundamental skills for playing winning poker is understanding and knowing how to calculate the pot odds.
In the first part of the article you’ll learn what pot odds are and how to calculate them. In the second part of the article we’ll go through some examples. You’ll also get a simple outs and equity cheat sheet. Enjoy!
What are pot odds?
Pot odds equals with the ratio between the size of the pot and the size of the bet against you. In other words this is the amount of chips in the pot in comparison to the amount of chips you just call to stay in the hand.
For example: if there are $200 in the pot and villain bets $100, then your pot odds are ($200+$100):$100 which is 3:1 (3 to 1). In other words you have to pay 1/3 pot in order to stay in the hand.
The mathematical foundation for calling situations in poker are Pot odds. In the absence of pot odds, it would be quite impossible to figure out which calls are profitable and which are not.
How to calculate the equity needed to make a profitable call?
We will use the same example from above: the pot is $200 and the villain bets $100, with the pot odds being 3:1. As the next step, in order to know exactly how much equity our hand needs to profitably call the bet, we need to convert our pot odds into a percentage.
First step is to calculate the total pot after our call, which in our case is :
$400 = $200(initial pot) + $100(bet of villain) + $100(our call)
Second step is to divide the size of the call with the total pot, which in our case equals:
0.25 = $100(our call) / $400(total pot)
Finally in order to get the percentage we just have to multiply it by 100:
0.25 * 100 = 25%
Conclusion: our hand needs more than 25% equity in order for the call to be profitable.
Shortcut for calculating your equity: The rule of four and two
First, here is the Number of Outs Cheat Sheet:
| Specific Draws | Number of outs | Equity(Turn and River) |
| Pocket pair to set | 2 | 8.4% |
| One overcard | 3 | 12.5% |
| Gutshot | 4 | 16.5% |
| Two overcards | 6 | 24.1% |
| Open-ended straight draw | 8 | 31.5% |
| Flush draw | 9 | 35% |
| Flush draw with one overcard | 12 | 45% |
| Flush draw with two overcards | 15 | 54.1% |
| Flush draw + Open-ended straight draw | 15 | 54.1% |
A useful shortcut to calculating the odds of completing a hand from a number of outs is the “rule of four and two”. You count the number of cards that will prove your hand, and then multiply the number by four to calculate your probability of catching that card on either the turn or the river. If you miss your draw on the turn, multiply your outs by two, to find your probability of filling your hand on the river.
Example: 5 outs give us about 20% equity (4% * 5).
In order to make your life easier, hit save on the next picture, a simple outs and equity cheat sheet, that covers the most common situations.
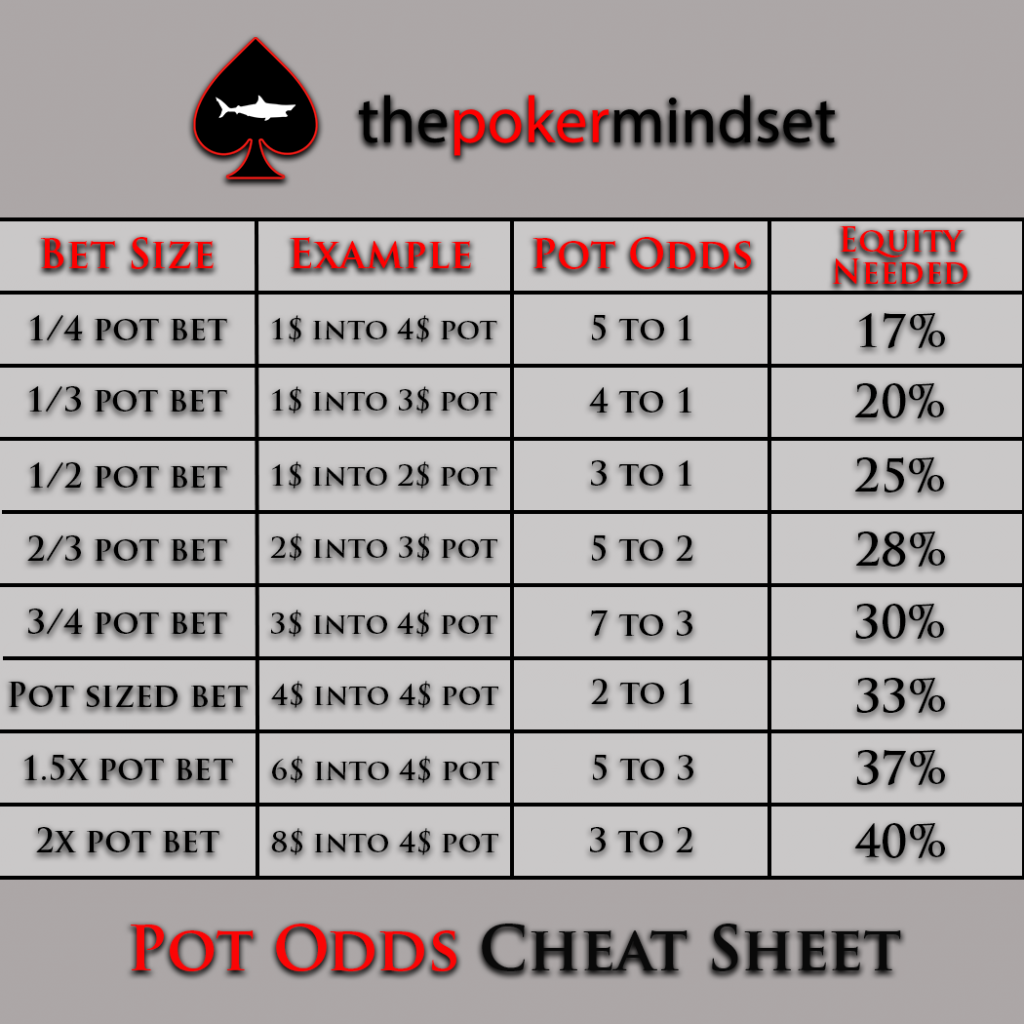
Example 1: Flush draw + Gutshot
In a $1/$2 No-limit game, we have 8♠ 9♠ in the Big Blind. Our opponent open-raises from the Dealer Position to $6. We are last to act and decide to call.
Flop comes: Q♠ 7♠ 5♦. We check and our opponent bets $8 into a $13 pot. Let’s go through our steps to figure out if we can profitably call.
First step is to calculate the total pot after our call, which in this case is:
$13(the pot size) + $8(the bet size) + $8(the call size) = $29
Second step is to divide the size of the call with the total pot, which in this case equals:
$8(the call size) / $29 (the final pot size) = 0.276
Finally in order to get the percentage we just have to multiply it by 100:
0.276 * 100 = 27.6%
This is the required equity to call.
Now the question is: Do we have enough equity to profitably call?
Let’s consider our outs:
- We have 9 outs to hit a flush, which according to our ‘rule of four and two’ means that we have around 18% chance to complete our flush draw on the turn.
- We also have a gutshot, which gives us an additional 3 outs(not 4, because one of our outs completes the flush draw). 3 outs equals another 6% chance.
- Finally we have 6 outs to hit a pair on the turn, giving us another 12% equity.
Note: Our opponent will not always bet the turn, which means that we can get a free river card.
Conclusion: You can see that we definitely have enough equity in order to profitably call.
Example 2: Gutshot
In a $1/$2 No-limit game, we have the same hand: 8♠ 9♠ in the Big Blind. Our opponent open-raises from the Dealer Position to $6. We are last to act and decide to call.
This time the flop is: Q♠ J♦ 5♦. Now we only have a gutshot and a backdoor flush draw. Our opponent bets half pot, $6.5 into a $13 pot. Let’s go through our steps to figure out if we can profitably call.
First step is to calculate the total pot after our call, which in this case is:
$13(the pot size) + $6.5(the bet size) + $6.5(the call size) = $26
Second step is to divide the size of the call with the total pot, which in this case equals:
$6.5(the call size) / $26 (the final pot size) = 0.25
Finally in order to get the percentage we just have to multiply it by 100:
0.25 * 100 = 25%
Do we have enough equity to call? Let’s consider our outs:
- We have 4 outs to hit our gutshot, which according to our ‘rule of four and two’ means that we have around 8% chance to complete our straight draw on the turn.
- The backdoor flush draw gives us some additional equity (around 4%), but we need two cards to complete it.
This time hitting a pair won’t improve our hand too much.
Conclusion: As you can see, in this example we don’t have enough equity to call, so we fold our hand.
Bonus: Other interesting poker odds
| Situation | Probability | Odds |
| Being dealt AA(or any specific pair) | 0.45% | 220 to 1 |
| Being dealt AK suited | 0.3% | 331 to 1 |
| Being dealt AK (any suit) | 1.2% | 82 to 1 |
| Being dealt TT, JJ, QQ, KK or AA | 2.3% | 43 to 1 |
| Being dealt a suited connector | 3.9% | 25 to 1 |
| Being dealt a pocket pair | 5.9% | 16 to 1 |
| Odds of flopping a flush | 0.8% | 118 to 1 |
| Odds of flopping a flush draw(holding suited hand) | 11% | 9 to 1 |
| Odds of flopping a set(holding a pocket pair) | 12% | 7.5 to 1 |
| Flopping a pair(matching one of our hole cards) | 29% | 2.45 to 1 |
| An overcard hitting the flop when we have TT | 69.5% | 0.44 to 1 |
| An overcard hitting the flop when we have JJ | 57% | 0.75 to 1 |
| An overcard hitting the flop when we have QQ | 41.4% | 1.42 to 1 |
| An overcard hitting the flop when we have KK | 22.6% | 3.42 to 1 |
Knowing when and how to calculate and use pot odds can put you well ahead of your opponents who are lazy to do the work. Congratulations for going through this article!
Recommended poker math books
- Essential Poker Math, Expanded Edition: Fundamental No-Limit Hold’em Mathematics You Need to Know
- Poker Workbook: Math & Preflop: Learn & Practice +EV Skills Between Sessions by James “Splitsuit” Sweeney
- Poker Math That Matters: Simplifying the Secrets of No-Limit Hold’em by Owen Gaines
- The Mathematics of Poker by Bill Chen
If you’re an online player and want to improve your poker game here is a must read article: What beginners and recreationals don’t know about tracking software?


